Es posible que haya escuchado antes el término "cadena de Markov", pero a menos que haya tomado algunas clases sobre teoría de la probabilidad o algoritmos informáticos. Cómo aprender a programar sin todo el estrés Cómo aprender a programar sin todo el estrés Quizás haya decidido seguir la programación, ya sea para una carrera o simplemente como un hobby. ¡Estupendo! Pero tal vez estás empezando a sentirse abrumado. No muy bien. Aquí hay ayuda para facilitar su viaje. Lea más, probablemente no sepa qué son, cómo funcionan y por qué son tan importantes.
La idea de una cadena de Markov es un concepto "bajo el capó", lo que significa que realmente no necesita saber cuáles son para beneficiarse de ellos. Sin embargo, definitivamente puede beneficiarse de la comprensión de cómo funcionan. Son simples pero útiles de muchas maneras.
Así que aquí hay un curso acelerado: todo lo que necesita saber sobre las cadenas de Markov condensadas en un artículo único y digerible. Si quieres profundizar aún más, prueba el curso gratuito de teoría de la información en Khan Academy (y considera otros sitios de cursos en línea también 8 Sitios web impresionantes para tomar cursos universitarios gratuitos en línea 8 sitios web impresionantes para tomar cursos universitarios gratuitos en línea Leer más).
Cadenas de Markov 101
Digamos que quieres predecir cómo será el clima mañana. Una verdadera predicción, del tipo realizado por meteorólogos expertos, 7 mejores aplicaciones meteorológicas gratuitas para Android, 7 mejores aplicaciones meteorológicas gratuitas para Android, y más, implicaría cientos, o incluso miles, de diferentes variables que cambian constantemente. Los sistemas meteorológicos son increíblemente complejos e imposibles de modelar, al menos para los legos como tú y como yo. Pero podemos simplificar el problema mediante el uso de estimaciones de probabilidad.
Imagina que tienes acceso a treinta años de datos meteorológicos. Empiezas desde el principio, notando que el día 1 estaba soleado. Continúas, notando que el Día 2 también estaba soleado, pero el Día 3 estaba nublado, luego el Día 4 llovía, lo que provocó una tormenta el Día 5, seguido de cielos despejados y soleados el Día 6.
Idealmente, sería más granular, optando por un análisis de hora por hora en lugar de un análisis de día por día, pero esto es solo un ejemplo para ilustrar el concepto, ¡tengan paciencia conmigo!
Haga esto durante todo el conjunto de datos de 30 años (que sería poco menos de 11, 000 días) y calcule las probabilidades de cómo será el clima de mañana basado en el clima actual. Por ejemplo, si hoy es soleado, entonces:
- Una probabilidad del 50 por ciento de que mañana vuelva a ponerse el sol.
- Una probabilidad del 30 por ciento de que mañana esté nublado.
- Una probabilidad del 20 por ciento de que mañana lloverá.
Ahora repita esto para cada condición climática posible. Si hoy está nublado, ¿cuáles son las probabilidades de que mañana salga el sol, la lluvia, la niebla, las tormentas eléctricas, las tormentas de granizo, los tornados, etc.? Muy pronto, tienes todo un sistema de probabilidades que puedes usar para predecir no solo el clima del mañana, sino también el del día siguiente y el día siguiente.
Estados de transición
Esta es la esencia de una cadena de Markov. Usted tiene estados individuales (en este caso, condiciones climáticas) donde cada estado puede realizar la transición a otros estados (por ejemplo, los días soleados pueden pasar a días nublados) y esas transiciones se basan en las probabilidades. Si desea predecir cómo será el clima en una semana, puede explorar las diversas probabilidades en los próximos siete días y ver cuáles son las más probables. Por lo tanto, una "cadena" de Markov.
Quién es Markov? Era un matemático ruso al que se le ocurrió la idea de un estado que conduzca directamente a otro estado basado en una cierta probabilidad, donde ningún otro factor influye en la oportunidad de transición. Básicamente, inventó la cadena de Markov, de ahí el nombre.
Cómo se usan las cadenas de Markov en el mundo real
Con la explicación fuera del camino, exploremos algunas de las aplicaciones del mundo real en las que son útiles. ¡Te sorprenderá descubrir que has estado utilizando las cadenas de Markov todo este tiempo sin saberlo!
Generación de nombre
¿Alguna vez has participado en juegos de mesa, juegos de MMORPG o incluso en la escritura de ficción? Es posible que haya agonizado al nombrar a sus personajes (al menos en un punto u otro), y cuando parece que no puede pensar en un nombre que le guste, es probable que haya recurrido a un generador de nombres en línea. Cree un nuevo alias con The Los mejores generadores de nombres en línea [Weird & Wonderful Web] crean un nuevo alias con los mejores generadores de nombres en línea [Weird & Wonderful Web] Tu nombre es aburrido. Afortunadamente, puede conectarse en línea y elegir un nuevo alias utilizando uno de los innumerables generadores de nombres disponibles en Internetz. Lee mas .
¿Te has preguntado alguna vez cómo funcionaron esos generadores de nombres? Resulta que muchos de ellos usan cadenas de Markov, por lo que es una de las soluciones más utilizadas. (¡Hay otros algoritmos que son igual de efectivos, por supuesto!)
Todo lo que necesita es una colección de cartas donde cada letra tenga una lista de posibles cartas de seguimiento con probabilidades. Entonces, por ejemplo, la letra "M" tiene un 60 por ciento de posibilidades de conducir a la letra "A" y un 40 por ciento de posibilidades de llevar a la letra "I". Haga esto para un montón de otras letras, luego ejecute el algoritmo. Boom, ¡tienes un nombre que tiene sentido! (La mayor parte del tiempo, de cualquier manera.)
Google PageRank
Una de las implicaciones interesantes de la teoría de la cadena de Markov es que a medida que aumenta la longitud de la cadena (es decir, aumenta el número de transiciones de estado), la probabilidad de que aterrice en un determinado estado converja en un número fijo, y esta probabilidad es independiente de donde comienzas en el sistema
Esto es extremadamente interesante cuando piensas en toda la red mundial como un sistema de Markov donde cada página web es un estado y los enlaces entre páginas web son transiciones con probabilidades. Este teorema básicamente dice que no importa en qué página web comiences, tu probabilidad de aterrizar en una determinada página web X es una probabilidad fija, asumiendo un "largo tiempo" de navegación .
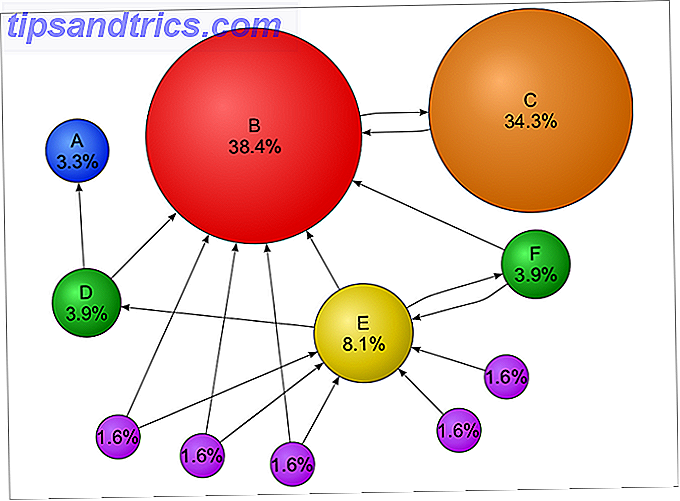
Y esta es la base de cómo clasifica Google las páginas web. De hecho, el algoritmo de PageRank es una forma modificada (léase: más avanzada) del algoritmo de la cadena de Markov.
Cuanto mayor sea la "probabilidad fija" de llegar a una página web determinada, mayor será su PageRank. Esto se debe a que una probabilidad fija más alta implica que la página web tiene muchos enlaces entrantes de otras páginas web, y Google asume que si una página web tiene muchos enlaces entrantes, entonces debe ser valiosa. Cuantos más enlaces entrantes, más valioso es.
Es más complicado que eso, por supuesto, pero tiene sentido. ¿Por qué un sitio como About.com obtiene una mayor prioridad en las páginas de resultados de búsqueda? Porque resulta que los usuarios tienden a llegar allí mientras navegan por la web. Interesante, ¿no?
Typing Word Prediction
Los teléfonos móviles han tenido tipeo predictivo durante décadas, pero ¿puedes adivinar cómo se hacen esas predicciones? Ya sea que estés usando Android (opciones de teclado alternativas) ¿Cuál es el mejor teclado alternativo para Android? ¿Cuál es el mejor teclado alternativo para Android? Echamos un vistazo a algunos de los mejores teclados de Play Store y los ponemos a prueba. Más) o iOS (opciones de teclado alternativas) 9 Teclados iOS alternativos para hacer que escribir sea más fácil o más divertido 9 Teclados iOS alternativos para hacer que escribir sea más fácil o más divertido Cuando Apple dejó de actuar como un padre sobreprotector e introdujo teclados de terceros, todos se fueron loco por el teclado. Lea más), hay muchas posibilidades de que su aplicación preferida use cadenas de Markov.
Es por eso que las aplicaciones de teclado preguntan si pueden recopilar datos sobre sus hábitos de escritura. Por ejemplo, en el teclado de Google, hay una configuración llamada fragmentos de acciones que le pide "compartir fragmentos de qué y cómo escribe en las aplicaciones de Google para mejorar el teclado de Google". En esencia, sus palabras se analizan e incorporan a las probabilidades de la cadena de Markov de la aplicación.
Es por eso que las aplicaciones de teclado a menudo presentan tres o más opciones, generalmente en orden de mayor a menor. No puede saber con certeza qué significa escribir a continuación, pero es correcto la mayoría de las veces.
Simulación Subreddit
Si nunca usaste Reddit, te recomendamos que al menos visites este fascinante experimento llamado / r / SubredditSimulator.
En pocas palabras, Subreddit Simulator incluye una gran cantidad de TODOS los comentarios y títulos hechos en las numerosas comunidades de Reddit, luego analiza la composición palabra por palabra de cada oración. Al usar esta información, genera probabilidades de palabra a palabra, luego usa esas probabilidades para venir a generar títulos y comentarios desde cero.
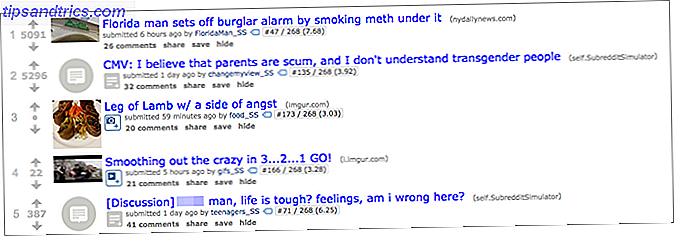
Una capa interesante de este experimento es que los comentarios y títulos son categorizados por la comunidad de la que provienen los datos, por lo que los tipos de comentarios y títulos generados por el conjunto de datos de / r / food son muy diferentes de los comentarios y títulos generados por / r / conjunto de datos de fútbol.
Y la parte más divertida (o tal vez la más inquietante) de todo esto es que los comentarios y los títulos generados con frecuencia pueden ser indistinguibles de los hechos por personas reales. Es absolutamente fascinante
¿Conoces otros usos interesantes para las cadenas de Markov? ¿Tienes alguna pregunta que aún necesita respuesta? Háganos saber en un comentario abajo!