Dado que el binario es tan absolutamente fundamental para la existencia de las computadoras, parece extraño que nunca antes hayamos abordado el tema, así que hoy pensé en dar una breve descripción de lo que realmente significa el binario y cómo se usa en las computadoras . Si siempre te has preguntado cuál es la diferencia entre 8 bits, 32 bits y 64 bits, y por qué es importante, ¡sigue leyendo!
¿Qué es binario? La diferencia entre Base 10 y Base 2
La mayoría de nosotros hemos crecido en un mundo de números base 10, lo que significa que tenemos 10 números 'base' ( 0-9 ) de los cuales derivamos todos los demás números. Una vez que los hayamos agotado, subimos un nivel de unidad, 10, 100, 1000, esta forma de contar está martillada en nuestros cerebros desde el nacimiento. De hecho, fue solo a partir del período romano cuando empezamos a contar en la base 10. Antes de eso, la base 12 era la más fácil, y la gente usaba los nudillos para contar.
Cuando aprendemos la base 10 en la escuela primaria, a menudo escribimos las unidades de esta manera:
Entonces el número 1990 en realidad consiste en 1 x 1000, 9 x 100, 9 x 10 y 0 x 1 . Estoy seguro de que no necesito explicar la base 10 más allá de eso.
Pero, ¿qué pasa si en lugar de tener una selección completa de 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 para trabajar con los números de base, qué pasaría si solo tuviéramos 0 y 1 . Esto se llama base 2 ; y también se lo conoce comúnmente como binario . En un mundo binario, solo puedes contar 0, 1, entonces necesitas pasar al siguiente nivel de unidad.
Contando en binario
Ayuda inmensamente si escribimos las unidades cuando aprendemos binario. En este caso, en lugar de multiplicar cada unidad adicional por 10, se multiplica por 2, lo que nos da 1, 2, 4, 8, 16, 32, 64 ... Para ayudar a calcular, podemos escribirlos así:
En otras palabras, el valor más a la derecha en un número binario representa cuántos 1. El siguiente dígito, a la izquierda de eso, representa cuántos 2's. El siguiente representa cuántos 4 ... y así.
Con ese conocimiento, podemos escribir una tabla de conteo en binario, con el valor de base 10 equivalente indicado a la izquierda.
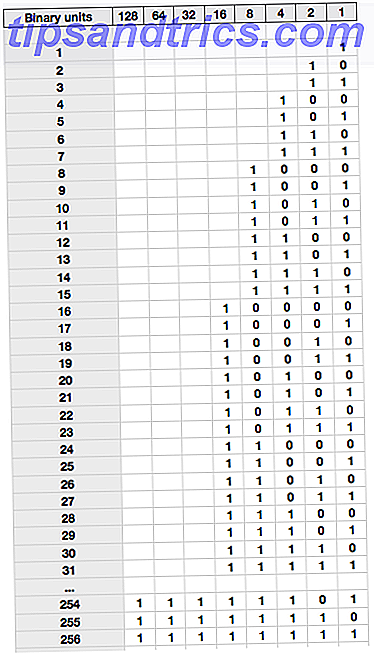
Dedique un momento a revisar eso hasta que pueda ver exactamente por qué 25 está escrito como 11001. Debería poder desglosarlo como 16 + 8 + 1 = 25.
Trabajando al revés - base 10 a binario
Ahora debería poder averiguar qué valor tiene un número binario dibujando una tabla similar y multiplicando cada unidad. Cambiar un número de base 10 regular a binario requiere un poco más de esfuerzo. El primer paso es encontrar la unidad binaria más grande que "encaje" en el número. Entonces, por ejemplo, si estuviéramos haciendo 35, entonces el número más grande de esa tabla que encaja en 35 es 32, entonces tendríamos un 1 allí en esa columna. Entonces tenemos un resto de 3, que necesitaría un 2, y finalmente un 1. Así que obtenemos 100011 .
8 bits, bytes y octetos
La tabla que he mostrado arriba es de 8 bits, porque tenemos un máximo de 8 ceros y unos para nuestro número binario. Por lo tanto, el número máximo que podemos representar es 11111111 o 255 . Esta es la razón por la cual para representar cualquier número del 0-255, necesitamos al menos 8 bits. Octet y Byte es simplemente otra forma de decir 8 bits. Por lo tanto, 1 byte = 8 bits .
Computación 32 vs 64 bit
En la actualidad, a menudo escuchas los términos versiones de Windows de 32 bits y 64 bits, y es posible que sepas que Windows de 32 bits solo puede admitir hasta 4 gigabytes de RAM . ¿Por qué es eso?
Todo se reduce al direccionamiento de la memoria. Cada bit de memoria necesita una dirección única para poder acceder a ella. Si tuviéramos un sistema de direccionamiento de memoria de 8 bits, solo podríamos tener un máximo de 256 bytes de memoria. Con un sistema de direccionamiento de memoria de 32 bits ( imagina extender la tabla de arriba para tener 32 columnas de unidades binarias ), podemos ir a cualquier lugar hasta 4.294.967.296 ? 4 billones de bytes, o en otras palabras - 4 bytes GIGA . La computación de 64 bits esencialmente elimina este límite al darnos hasta 18 trillones de direcciones diferentes, un número que la mayoría de nosotros simplemente no puede comprender.
Direccionamiento IPv4
La última preocupación en el mundo de la informática es acerca de las direcciones IP IPv6 & The Coming ARPAgeddon [Explicación de la tecnología] IPv6 & The Coming ARPAgeddon [Explicación de la tecnología] Lea más, en particular las direcciones IPv4, como estas:
- 192.168.0.1
- 200.187.54.22
En realidad, constan de 4 números, cada uno representa un valor de hasta 255. ¿Puedes adivinar por qué? Sí, la dirección completa está representada por 4 octetos ( 32 bits en total ). Esto parecía una gran cantidad de direcciones posibles ( alrededor de 4 mil millones de hecho ) en el momento en que se inventó Internet por primera vez, pero ahora estamos agotando rápidamente que todo en nuestra vida necesita estar conectado. Para resolver esto, el nuevo IPv6 usa 128 bits en total, lo que nos da aproximadamente 340 direcciones de undecillion ( poner 38 ceros en el extremo ) para jugar.
Voy a dejarlo allí por hoy, para poder volver a mi objetivo original, que era escribir el próximo tutorial de Arduino, en el que hacemos un amplio uso de un registro de desplazamiento de bits. Espero que hoy te haya dado una comprensión básica de cómo el binario es tan significativo para las computadoras, por qué siguen apareciendo los mismos números y por qué el número de bits que tenemos para representar algo limita la cantidad de memoria, el tamaño de la pantalla, el posible color valores, o direcciones IP únicas disponibles para nosotros. La próxima vez, echaremos un vistazo a los cálculos de lógica binaria, que es prácticamente todo lo que hace un procesador de computadora, y cómo las computadoras pueden representar números negativos.
¿Comentarios? ¿Confusión? ¿Encontraste mi explicación fácil de entender? En cualquier caso, póngase en contacto en los comentarios. ¡Te dejaré con una broma binaria!
Solo hay 10 tipos de personas en el mundo: los que entienden el binario y los que no.
Crédito de la imagen: Shutterstock